金融工学への誘い(その6)…ブラックショールズ微分方程式の具体的活用法
ブラックショールズ・モデルは、フィッシャー・ブラックとマイロン・ショールズの2人によって与えられました。その公式はそれを検証したロバート・マートンによってブラック・ショールズ公式と命名されました。ブラックは1995年に他界しましたが、ショールズとマートンはこの公式によって1997年にノーベル経済学賞を受賞しました。
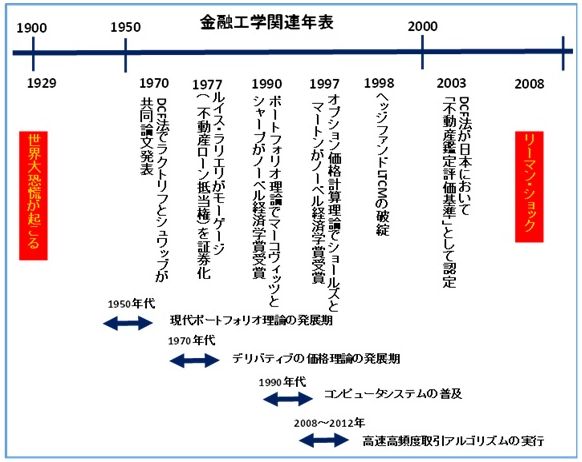

金融取引にはデリバティブと呼ばれているタイプの取引がありますが、ブラック・ショールズモデルは、そのデリバティブの中で最も難解と言われているオプション取引のために編み出された計算式なのです。
資産価格は、その資産の価値を評価することによって計算されます。資産価値とは、資産を持つことで得られる利益を意味します。ドルコール・オプションのような通貨オプションも、あるいは株式についてのオプションも、やはり資産の一種ですから、それを保有することで得られる利益を計算すれば、それがそのオプションの価格となります。
オプションはある条件下で特定の期間内に資産を買う、あるいは売る権利を与える有価証券です。オプションは自由に加工がしやすく、自在に組合せできるため、複雑な金融取引を生み出しています。そして、群を抜いて難解とされているのがオプション価格の計算です。
下図にブラック・ショールズモデルによるオプション価格の方程式を示します。ブラック・ショールズモデルは、正規分布に従って変動する資産価値から派生するオプション価格を、微分方程式を解くことによって求めたものです。
具体的には、まずポートフォリオの考えをベースにして微分方程式を設定し、その微分方程式を解くに当っては、資産価格の変動をランダムウォークという数学モデルで与え、またオプション価格については、境界条件という数学的テクニックを用いて、対象資産のオプション価格を求める式を誘導しています。

計算式においてポイントとなるのは、ボラティリティと呼ばれる変数だけで、あとは取引の条件を示すものであったり、容易に計算できるものばかりです。ボラティリティは、株価や円相場などの原資産価格の変動の激しさを示すもので、確率分布のばらつき具合を計る数値で、いわゆる標準偏差のことです。
ヨーロピアン・コールオプションの価格を求める例題を取り上げます。ここでヨーロピアン・スタイルとは、「満期日にしか権利行使できないオプション」を指し、アメリカン・スタイルの「満期までの期間中いつでも権利行使できるオプション」と区別します。
条件:現在の株価 S=14500円
権利行使価格 X=14000円
オプションの期間 2ケ月
ボラティリティ σ=38%
非危険利子率 r=6%
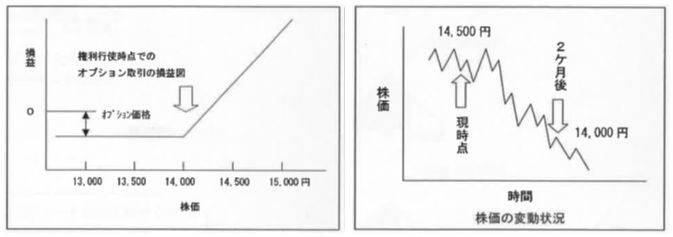
解答:
ブラック・ショールズモデルによる価格の計算式は下記で与えられます。

この程度の計算であれば、ポケットコンピュータがあればすぐに求まります。従って、この式を計算できるのでとできないのでは、交渉の場での優位性に大きな差がつきます。ポイントは、ボラティリティをどれほど精度よく予測できるかにかかっているように見えますが、皆さんどう思われますか。