金融工学への誘い(その7)…ブラック・ショールズ微分方程式の解法に挑戦
ブラックショールズ・モデルは、フィッシャー・ブラックとマイロン・ショールズの2人によって与えられました。その公式はそれを検証したロバート・マートンによってブラック・ショールズ公式と命名されました。ブラックは1995年に他界しましたが、ショールズとマートンはこの公式によって1997年にノーベル経済学賞を受賞しました。
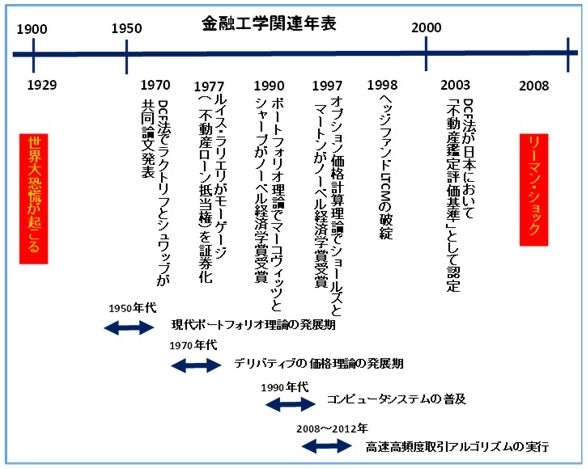


今回は、石村貞夫+石村國子著「金融・証券のためのブラック・ショールズ微分方程式」から、オプション価格の数学的取扱いについて、そのエッセンスを紹介します。
まず、下記の(A)にブラック・ショールズの偏微分方程式を、また(B)にその偏微分方程式を解いて求めたオプション価格の計算式を示します。ここで知りたいのは、
(1) どうして株価Sのオプション価格f (S, t)が、(A)式の偏微分方程式の形で表現できるのか?
(2) もし、表現できるとすれば、(A)式の偏微分方程式をどのように解いて(B)のオプション価格を求めることができるのか?
という2点に集約されます。

(1) の「どうして株価Sのオプション価格f (S, t)が、(A)式の偏微分方程式の形で表現できるのか?」という点ですが、下記のステップを追うことでそのエッセンスを味わうことができます。
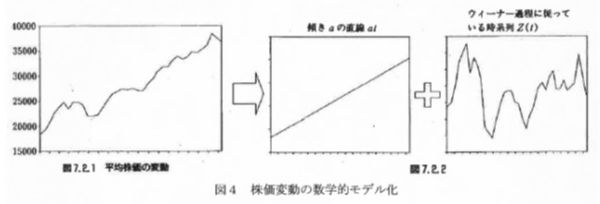
Step1. 株価Sが伊藤過程に従うと考えます。ここでのポイントはランダムウォークする株価Sが時間に比例する部分とウィナー過程の部分の合成で数学的に表現できる点です。ウィーナ過程とは、ランダムウォークの極限の形を言います。伊藤過程とはそのウィーナー過程を更に変形したものです。

(2) の「もし、表現できるとすれば、(A)式の偏微分方程式をどのように解いて(B)のオプション価格を求めることができるのか?」という点ですが、下記のようになります。


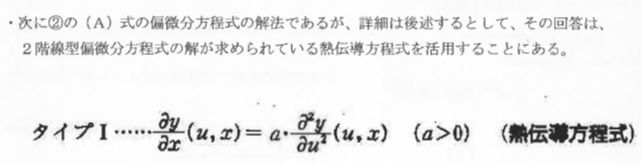
株価変動問題を熱伝導問題に置き換えて、偏微分方程式を解くなどは、凡人にできる技ではありません。さすがはノーベル学賞受賞したてだけのことはありますが、皆さんはどう思いますか。