学習教室講師の世界(その6)…幾何証明問題へのアプローチ方法

三重県県立高校の数学受験問題を見ていると、ここ数年の出題傾向として、最後にかなり難解な幾何の証明問題が出題されています。これをどう克服するかが、受験生の合否の大きな分かれ目になると感じます。今回、私なりに対策を考えてみましたが、幾何の証明問題では使われるパターンを覚えるのが良いように思われます。
Ⅰ. 平成30年度幾何学問題
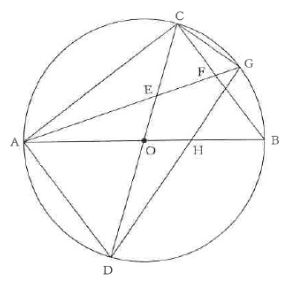
(1) 合同証明問題(H30)
△AOE≡△DOH
・円の半径の線分は等しい AO=DO
・対頂角は等しい ∡AOE=∡DOH
・∡CABの二等分線より ∡CAG=∡BAG
・弧CGの円周角 ∡CDG=∡CAG=∡BAG
・故に、1組の辺とその両端の角
(2) 相似証明問題(H30)
△ADH∽△GCE
・既出の合同条件対応する角度は等しい ∡AEO=∡DHO
・対頂角が等しい ∡AEO=∡CEG
・△ADO二等辺三角形 ⇒ 底角は等しい ∡OAD=∡ODA
・弧ACに対する円周角 ∡ADC=∡AGC
・2組の角度がそれぞれ等しい
(3) 線分OEの長さ
・条件よりAB=10cm、BC=6cm
・直径に対する円周角は90度
・三平方の定理 辺AC=8cm
・∡Aの二等分線から底辺の比を求める AC:AO=CE:EO
・円の半径を比で分ける
(4) 線分AEと線分EGの長さの比
・方針として2つの三角形の相似の比を活用する
・相似となる三角形を見付ける △EAC=△EGO
・相対する辺の比 AC:AO=8:5
(5) △ADHと△GCEの面積比の問題
・面積比と底辺の関係を用いる
・△GEC:△AEC=5:8
・△AEC:△AOE=8:5
・△AOE:△ADO=5:13
・△ADO:△ADH=13:18
・△GEC=5/8×△AEC=5/8×8/5△AEO=5/8×8/5×5/13×13/18△ADH
Ⅱ. 平成29年度幾何学問題
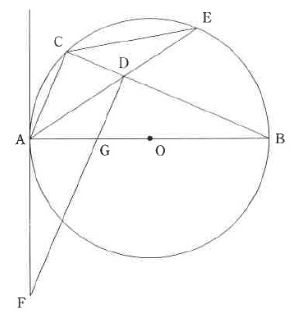
(1) 相似証明問題(H29)
△ACE∽△CDE
・∡Eは共通
・線分AEは∡CABの二等分線 ∡CAE=∡BAE
・弧BEに対する円周角は等しい ∡BAE=∡BCE
・故に、2組の角がそれぞれ等しい
(2) 合同証明問題(H29)
△AGF≡△DGB
・対頂角より ∡AGF=∡BGD
・円の接線は半径に垂直 ∡GAF=90°
・DF∥CAより同位角 ∡ACB=∡GDB
・半円の弦に対する円周角は90度 ∡ACB=90°
・DF∥ACより錯角 ∡CAD=∡ADG
・線分ADは∡CABの二等分線 ∡CAD=∡GAD
・△GADは二等辺三角形 AG=DG
・故に、一組の辺とその両端の角が等しい。
(3) 線分AGの長さ
・条件よりAB=10cm、AC=4cm,
・△BGD∽△BAC AB:GB=AC:GD ⇒ GD=20/7
・△AGDは二等辺三角形 AG=GD=20/7
(4) △CDEと△AGFの面積比
・△ACBと△GDBより平行線と線分の比 AB:AG=CB:CD ⇒ CD=4/7√21
・△CDE∽△ACEより△ACE=7/3△CDE
・△ACD=△ACE-△CDE=7/3△CDE-△CDE=4/3△CDE
・△ABD=5/2△ACD=5/2・4/3△CDE
・△GDB=5/7△ABD=5/2・4/3・5/7△CED
・△AGF=△GDB=5/2・4/3・5/7△CED
・△CDE:△AGF=1:50/21=21:50
・△ABD=5/3△ADC △ABD=5/8△ABC
・△ABC=8/3△ADC △ADC=3/8△ABC
Ⅲ. 平成28年度幾何学問題
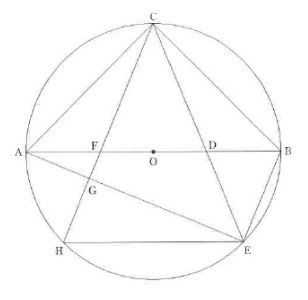
(1) 相似証明問題(平成28)
△ADC∽△CDF
・∡Dは共通な角
・弧BCに対する円周角 ∡BAC=∡BEC
・BE∥CHより錯角が等しい ∡BEC=∡FCE, ∡FCD=∡BAC
・2組の角がそれぞれ等しい
(2) 合同証明問題(H28)
△AED≡△CEB
・仮定…AC=BC, AC=AD ⇒ BC=AD
・弧BEに対する円周角 ∡BCE=∡BAE
・弧ACに対する円周角 ∡AEC=∡ABC
・三角形で2つの角が等しければ残りの角も等しい ∡ADE=∡BDC
・故に、1組の辺とその両端の角が等しい
(3) 線分EH
・AO=4cm
・△ABCは直角二等辺三角形 ⇒ AB⊥CO
・三平方の定理から AC=4√2
・円弧BCに対する円周角は等しい ∡BAC=∡BEC=45°
・CH∦BEより錯角が等しい ∡BEC=∡HCE=45°これは弦EHの円周角
・弦EHの中心角は∡HOE=90°EH=4√2
(4) △CGEの面積
・△ACF≡△BCD前提
・△CGE=△CHE-△GHE
・△CHEの面積=1/2×底辺4√2×高さ(4+2√2)=8+8√2
・△GHEの面積は△ABEとの相似関係から求める
・相似比 AB:HE=8:4√2=1:4√2/8=1:√2
・面積比 △GHE:△ABE=(12):(√22)=1:2
・△GHEの面積=1/2×△ABE=1/2×1/2×(8×2√2)=4√2
・△CGE=△CHE-△GHE=8+8√2-4√2=8+4√2
Ⅳ. 平成27年度幾何学問題
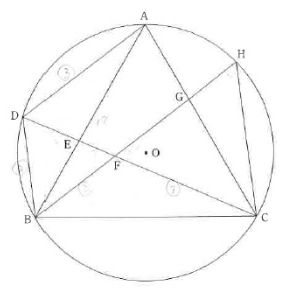
(1) 合同証明4(H27)
△ADB≡△CFB
・仮定 AD=CF
・△ABCは正三角形だから、辺の長さは等しい AB=BC
・弧BDに対する円周角 ∡BAD=∡BCD
・故に、2組の辺とその間の角が等しい
(2) 相似証明(H27)
△BFE∽△CHG
・弧AHに対する円周角 ∡ABH=∡HCA
・△ADB≡CFBより、対応する辺は等しい BF=BD
・△BFDは二等辺三角形 ∡BDF=∡BFD
・弧BCに対する円周角 ∡BDC=∡BHC
・故に、2組の角がそれぞれ等しい
(3) 線分CEと線EDの長さの比
・与えられた条件 AB=10cm, AB : DB=3:2
・△ADB≡△CFBより、BD=BF、∡DBF=∡EBC=60度 (△ABC:正三角形)
・△DBFは正三角形になり、∡BFD=60度
・また、弧ACの円周角より、∡ADF=∡ABC=60度
・∡ADF=∡DFB 錯角は等しいのでAD∥BF
・△ADE∽△BFEより、DE:FE=AD:BF=3:2 よってDE:EF=3:2
・AD=CF=③、DB=BF=FD=②、DE : EF=[3] : [2]
・DE=②×[3]/[5]、EF=②×[2]/[5]
・DE : EF : FC=②×[3]/[5] : ②×[2]/[5] : ③=6 :4 : 15
・DE : EC= 6 :19
(4) △CFBの面積
・△ABCは正三角形なので、頂点Aから辺BCに垂線を引き、その交点をIとする。
・△ABIは60度の角度を持つ直角三角形なので、三平方の定理より、AI=5√3
・よって△ABC=25√3
・△ADE∽△BFEで相似比は3:2より、△EBC=2/5△ABC=10√3
・CF:FE=15:4より△CFB=15/19△EBC
Ⅴ. 平成26年度幾何学問題
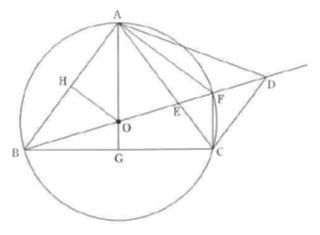
(1) 相似証明(平成26)
△AOH∽△ABG
・共通な角 ∡OAH=∡BAG
・仮定 ∡AOH=1/2△AOB
・1つの弧に対する円周角と中心角の関係より、∡ACB=1/2∡AOB
・∡AOH=∡ACB
・△ABCは二等辺三角形だから、∡ABG=∡ACB、∡AOH=∡ABG
・故に、2組の角がそれぞれ等しい
(2) 合同証明問題(平成26年)
△ACF≡△ADF
・共通 AF=AF
・仮定から AC=AD
・△ACDは二等辺三角形より、∡ACD=∡ADC
・△ABDは二等辺三角形より、∡ABD=∡ADB
・弧AFに対する円周角の大きさは等しいから、∡ABF=∡ACF
・∡ACF=∡ADB、∡FCD=∡FDC
・△FCDは二等辺三角形より、FC=FD
・故に、3組の辺がそれぞれ等しい
(3) 線分OG
・条件より AB=10cm, BC=12cm
・△ABCは二等辺三角形なので頂点Aの二等分線は底辺と直角に交わる
・直角三角形ができれば、三平方の定理で計算可能。 ⇒ AG=8
・△AOH∽△ABGより、AH:AG=AO:AB ⇒ AO=25/4
・よってOG=7/4
(4) △AEFと△ADFの面積比
・△BFCでの中点連結定理より、FC=2OG, OG∥FC ⇒ よってFC=7/2
・OG∥FCより、△AOE∽△CFE ⇒ AE:CE=AO:CF=25:14
・よって△AEF:△CEF:△ACF=25:14:39
・△ACF≡△ADFより、△AEF:△ADF=25:39
幾何の証明問題は、その証明ルートを幾つかのパターンに分類できることが分りました。このパターンを覚えてしまうことが、幾何の証明問題をクリアする1つの方法であると思いますが、皆さんどう思われますか。