学習教室講師の世界(その11)…数学と物理の融合
高校の数学には、微分、積分、ベクトル、数列、複素数といったものがあります。現実の世界で高校生に数学を教えていますと、このようなものが実世界でどの様に役立つのですかという質問が必ず出て来ます。そこで、今回は数学が物理の世界でどのように応用されているのかを調べてみました。
数学的思考を行なう神と数学の定理
数学における定理とは何なのかを考えてみたいと思います。例えば、ピタゴラスの定理は皆さん良く知っています。直角三角形において、底辺2+高さ2=斜辺2というあの定理です。この定理はBC572年に発表されました。
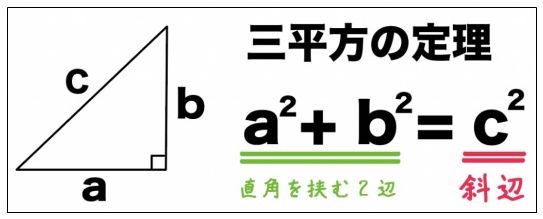

定理は「永遠・不変の存在」であり、「永遠・不変の世界」に属するものだと考えられます。ピタゴラスは、「永遠・不変の世界」は、「神の世界」であり、永遠・不変な存在を対象とする数学は、神の思考であると考えました。このようにして、「数学」と「信仰」が結び付いたのです。
「数学的な思考を行う神」の存在を確信したピタゴラスは、次に音楽が人間の精神に影響を与えることに注目しました。ピタゴラスにとって、精神は神の世界を感知するものですから、その精神に影響を与える音楽にも、神秘的な性質があるのではないかと考えました。そして、どのような音楽を聞くと、精神が「快」と感じるか実験しました。

実験に用いたのは、一弦琴(モノコルト)という弦楽器です。一弦琴を使った実験では、まず、弦全体の出す音が聞き取られ、次に、この音と一緒に聞いた時に「快」だと感じる音(協和音)を探しました。その結果、基準になる弦の長さが整数比をなすときに協和音になることが分りました。基音、4:3、3:2、2:1です。
まず、「整数比」という「数学的性質」は、ピタゴラスにとって神の世界に属するものです。ですから、「整数比」が協和音の実験によって見出されたということは、神の世界が、人間が勝手に作り出したフィクションではなく、確かに実在するという証明だと感じられたのではないでしょうか。
そして、それが人間の精神が「快」という感覚として感知できるということは、人間の精神が神の世界と確かに繋がっていて、精神が神の世界を感知する器官となっていることの証明だと感じたのではないでしょうか。
天体観測から生まれた三角比
三角比は天文学と共に発達して来ました。エジプトでは、ナイル川のほとりで前5,000年から農耕が始まります。ナイル川が毎年洪水を起こし、上流から栄養分をたくさん含んだ土が流れてくるため、土地が肥沃で農耕に適していたのです。
エジプト人にとっては、いつナイル川が増水するかがとても大きな関心事です。なぜなら、それに合わせて農耕の準備をするからです。彼等はナイル川の増水時期を知るために天体に着目しました。そして、7月の半ば、明け方の東の地平線ぎりぎりにシリウスがひときわ輝く時がある。丁度、その時からナイル川が増水することを発見しました。翌年同じ場所にシリウスが輝くまでが365日かかることを発見し、太陽暦を作成します。
天体をプラネタリウムのような球面に張り付いているものだと考えると、天球に張り付いた天体の位置を表すのには「角度」が2つあれば十分です。この様にして、「角度を測定し、天体の位置を知る」ことが行われる様になって来たのです。「角度」という量は、「天体」と密接に結び付いていたのです。
エジプトとメソポタミアに起こった文明を吸収して、地中海沿岸にギリシャ文明が発展します。ギリシャ人は、角度と長さの対応関係が分れば、「角度を測定して距離を計算する」ことが出来るということに気付きました。
アリスタルコス(前310頃~前230頃)は、「角度を測定して、距離を測る」というやり方で、地球と太陽の距離と、地球と月の距離の比を計算しました。アリスタルコスは、月が半月に見える時の太陽と月のなす角を測定しました。アリスタルコスは、太陽と半月、地球を頂点とする直角三角形の辺の比を計算しようとしました。

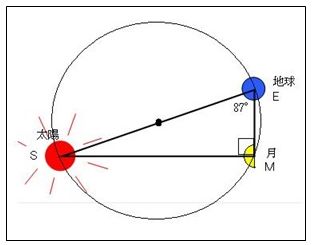
「直角三角形における角度と辺の比の対応関係」のことを三角比と呼びます。アリスタルコスの例でも分るように、三角比が分れば、角度を測定することで、距離の比を計算することができます。もし、3つの辺のうちの1つの長さが分っていれば、他の辺の長さも計算可能になります。
具体的には、地球は365日で太陽の周りを一周します。今地球の速度が測定できれば1日に地球がどれだけ動くかが分りますので、、公転軌道の円周の長さが求められます。そうすれば、地球と太陽の距離は自ずと分ります。
「角度を測定し、距離を求める」という方法は、測量技術として利用され、土地の広さを測定したり、建物を建てたりすることにも利用されています。
フィボナッチ数列と黄金比の繋がり
1-1-2-3-5-8-13-21はフィボナッチ数列ですが、最後の21と13の比は1.615で、この項数を増やして行くと、この比が1.618に近づくという訳です。
そして、驚嘆すべきは、黄金比が自然界の事物の基本的な構成に深く関わっていることです。植物や動物、そして人間についてさえも、さまざまなものの比率が不気味なほどの正確さで1.618対1に迫っています。
「黄金比はいたるところに見られます。偶然の域を超えているのは明らかで、だから古代人はこの値が万物の創造主によって定められたにちがいないと考えました。古の科学者はこれを“神聖比率”と呼んで崇めたものです。

物体の運動を決めるベクトル
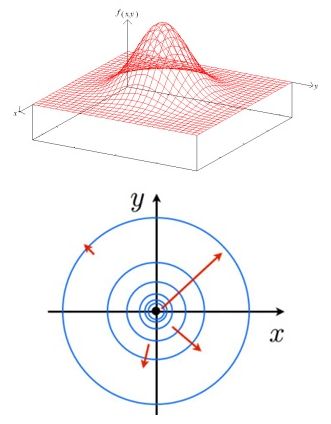
物体の運動を表す位置、速度、加速度といった量や、物体に働く力は、「向きと大きさを持つ量」です。このような量は矢印で表すと便利です。「ベクトル」は、この「矢印で表せる量」についての数学なのです。
山のある地点(x、y)に立ってぐるりと四方八方を見回した時に、最も急峻な傾きのある方向に、そのベクトルの先は向いているのです。言い換えれば、そこにボールをそっと置いた時に、そのボールが転がり落ちて行く方向が、勾配ベクトルの方向です。なぜなら、重さのある物体は、より低い所へと向かうのが自然の法則なのですから。
瞬間速度を定義する道具が微分
瞬間の速度は、ニュートンが「微小量」という概念を導入し、微分・積分学を作り上げて始めて定義することができるようになります。
速さが変化する運動、例えば物体の落下運動、斜面での物体の運動で、ある時刻における瞬間の速さf(x)をどう求めるのか。P点に対し曲線に沿って微小時間hだけ正方向にずらした点をQ点とします。2点を結んだ直線の傾きを計算してみますと、
速さの差分={f(x+h)-f(x)}/h
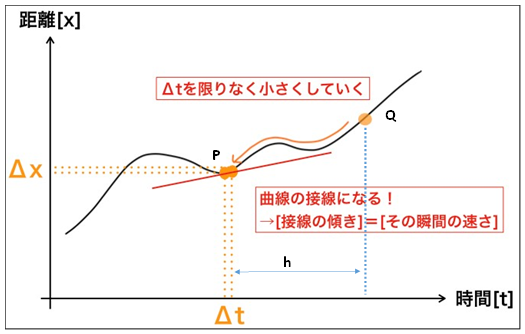
今、求めたいのは、時間tにおける瞬間の速さですから、hの値をどんどん小さくして行きます。この時、グラフ上でQ点はP点にどんどん近付いて行き、PQを結ぶ直線は、P点における接線にどんどん近付いて行きます。そして、hを限りなく0に近付けた時、PQを結ぶ直線は、Pにおける接線に限りなく近づきます。
このようにして、求めた vは、tにおける接線の傾きに果てしなく近付けることができるような値です。
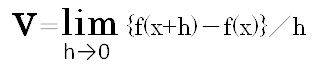
瞬間速度から移動距離を求める道具が積分
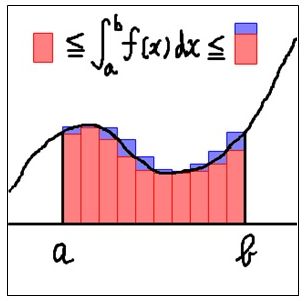
滑らかな斜面上でカーリングを静かに放して滑らせた時のストーンの移動距離を求めてみます。ストーンの速度をv(m/s)、ストーンを放した時を0とした時刻をt(秒)とすると、今度は時間とともに次第に速度が大きくなって行き、時刻と速度の関係を表したグラフが次の様になっています。
このグラフから、t=0からt=4までの間にストーンが進んだ移動距離を求めてみます。
移動距離=速度×時間
という関係は、速度が一定の時に成り立つ関係ですので、今回の様に、速度が刻一刻と変化している時には成り立ちません。そこで、分割された面積の足し合わせを0秒から4秒まで行って、4秒後の移動距離を求めます。
この様に、限りなく細かく分割した長方形の面積を無限個足し合わせることで面積を求める方法を区分求積法と言います。ここでも「微小量」が活躍します。
ミクロな物質の波動を表す道具が虚数
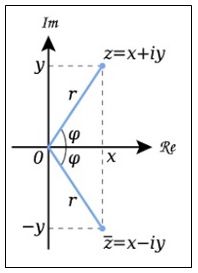
電子のようなミクロなものは、粒子でもあり、波でもあるという二重性を持っています。虚数を考えることは、波を考えることです。虚数などという抽象的なものを想像するには、骨が折れますが、一旦、eiθを(三角関数と同じく)波を表す道具と考えてしまえば、計算の技術上は三角関数のcosよりも極形式のeiθの方が、よっぽど便利に使えます。
数学の複素解析におけるオイラーの公式とは、複素指数関数と三角関数の間に成り立つ以下の恒等式のことです。
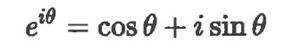
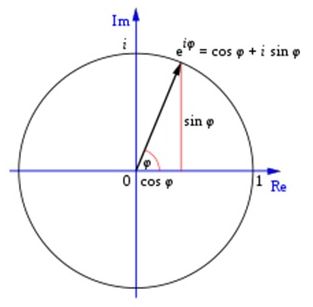
交流では、電源装置の働きによって、電流の向きが周期的に変化します。これが周りの磁気の変化を生み、またそれが電流の変化を生みます。これが空間を伝わると電磁波になります。電磁波とは、「電気と磁気の波」という意味です。
交流では、抵抗に相当するものがインピーダンスですが、交流のインピーダンスは、実部と虚部を持つ複素数で表されるのが普通なのです。実在する交流の抵抗が複素数で表されて、虚数が現実の世界に入り込んで来るということは大変な驚きです。

私は、虚数なんてものは数学のトリックに過ぎないと思っていたのですが、量子力学では物理的な実体に関係しているのです、虚数空間はどらえもんの「どこでも扉」の扉を開くと、別の世界があるという感覚を学びました。
標準偏差・分散・正規分布から求める偏差値
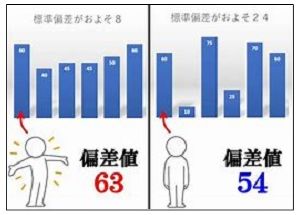
通常、多くの受験生は全国的な模擬テストに参加して、その得点と偏差値から希望する大学に入学できるのかどうかを判断します。講師の側としては、この偏差値はデータ分析と正規分布の問題でもあることから、偏差値がどの様な意味を持ち、どの様に求められているかを正しく理解しておくことは非常に重要と考えています。
なお、偏差値の求め方の詳細は本シリーズ(その3)…「偏差値の意味と求め方」で紹介していますので参照下さい。
投資信託の安全性を証明する大数の法則
投資信託はどうして安全なのかを数学的にひも解くことができます。本シリーズ(その14)…「投資信託の安全性を数学的にひも解く」で詳細を紹介しますので楽しみにして下さい。
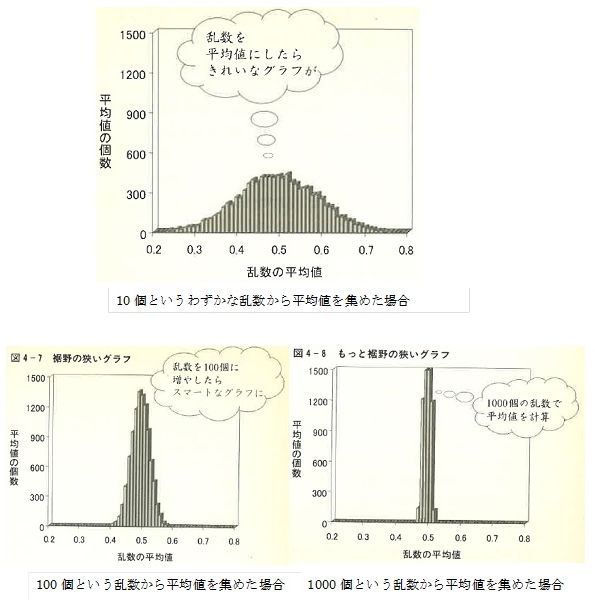
要は、図に示すように、採択する乱数の個数が多くなるほど、乱数が集まったそれぞれの群の平均値のばらつきは小さくなり、0.5に限りなく近づいて行きます。これが大数の法則です。デタラメの乱数の話をしているのに、乱数の数が増えるほどその平均値はどんどん一定値に近づくという、手品にあっているような感覚ですが、この特性が投資信託安全という話に繋がります。
結局、乱数とは、次に何が現れるかは予測はできませんが、全体としては他の数の集合と同じで、平均値やそのバラツキ等の統計的処理を適用できる数の集まりだと言えるという点がポイントです。
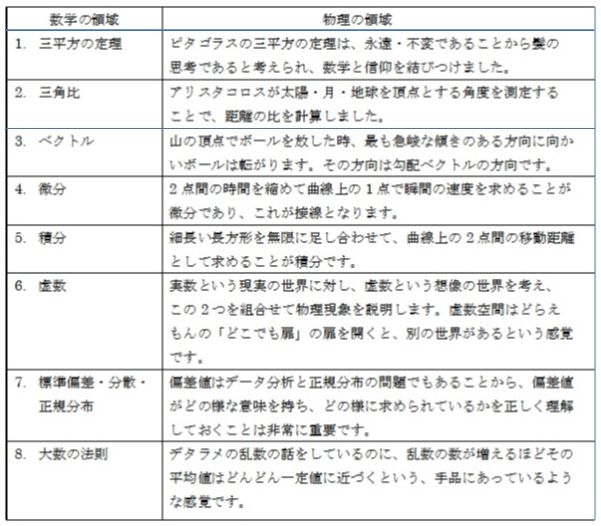
今回、下記6項目については現実の物理現象がどのような数学と結び付いているかを知ることができました。
なお下記の文献を参考にしています。
岸野正剛「今日から使える物理数学」講談社
岡田正彦「考え方がつくやさしい数学」講談社
丹羽敏雄「数学は世界を解明できるか」中央新書
数学の講師としては、生徒の質問、「すなわち現実の世界でどのように活用されているのか」についてきっちりと答えてやる必要がありますが、皆さんどう思われますか。