高齢期の投資戦略(その5)…投資信託の安全性を数学的にひも解く
投資には、「企業の株を買う株式投資」と「プロが運用してくれる投資信託」があります。後者の投資信託は、金融の専門家が数百種類の株や債券を選び、セットにして販売するものです。それを小分けにした商品をファンドといいます。中身は主に株です。

しかし、投資信託と株の売買が決定的に異なるのは、投資信託は安全性が高いことです。それはなぜかを数学的にひも解いてみます。岡田正彦著「考える力がつくやさしい数学」を参考にしました。
著者は、まえがきの中で「株や投資信託を持っている人は、景気の変動を予想してみたくなります。近年、数学の応用で、もっとも進歩したものの1つが予測です。過去の変動から情報を読み取り、それをもとに将来を予測することもできます。」と述べています。
さて、、株価の変動は誰も予測することができません、このように予測できないものを数学的に扱う時はいつも「モンテカルロ法」が登場します。すなわち「モンテカルロ法」とは、計算式がわからないような出来事を、乱数とシミュレーション計算や数値計算を使って再現したり、答えを求めようとするものです。
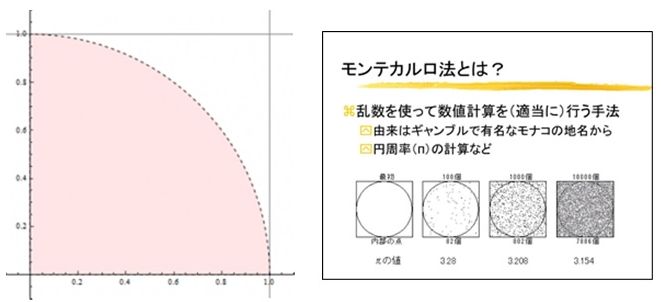
例として、モンテルロ法を使った円周率πのシミュレーションを紹介します。図に示すように一辺が長さ1の正方形の内側に内接する四分の一の円を描きます。正方形内でランダムな点をN個発生させて、そのうちの四分の一の円の中に入る点の数Sを数えます。ランダムな点を多数発生させれば、Nは正方形の1に対応し、Sは半径1の単位円の四分の一の面積 πr2×1/4=π・12×1/4=π/4 に対応します。
結果は、100個であればπ=3.28、1,000個であれπ=3.208、10,000個であればπ=3.154となり、個数が増えるほどπの値3.1415に近づくことを示しています。
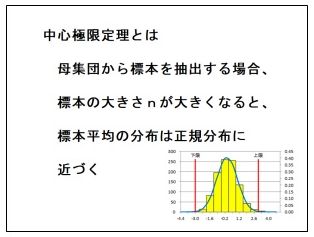
中心極限定理というものがあります。これは「母集団の分布がどのようなものであっても、確率変数の和の分布の形は標本の大きさが大きいときは、正規分布で近似できる」というものです。中心極限定理によりますと、標本の数がm倍になると、バラツキを表す標準偏差が1/√mになることが分かっています。例で示した結果は、中心極限定理が正しいことを物語っています。
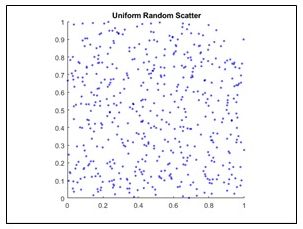
ここで乱数という言葉が出てきましたので、この乱数の性質を考えます。デタラメな数字の集まりを「乱数」といいます。現代では、乱数をコンピュータで作るのが普通です。しかし、乱数を発生させる方法も千差万別で、決定版というものはありません。そして、この出鱈目な数字は案外なところで役に立つものです。
ここで0から1の間に均等に散らばるように作られた乱数を考えます。しかし、不思議な事に無数の乱数から平均値求めれば、いつも0.5に限りなく近くなります。図は採択する乱数の個数を10個、100個、1000個と変化させたときの、平均値のバラツキを示したものです。
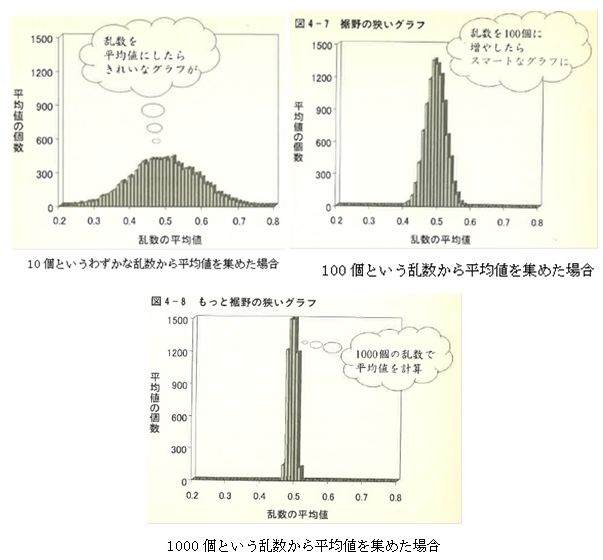
図に示すように、採択する乱数の個数が多くなるほど、乱数が集まったそれぞれの群の平均値のばらつきは小さくなり、0.5に限りなく近づいて行きます。デタラメの乱数の話をしているのに、乱数の数が増えるほどその平均値はどんどん一定値に近づくという、手品にあっているような感覚ですが、この特性が投資信託安全という話に繋がります。結局、乱数とは、次に何が現れるかは予測はできませんが、全体としては他の数の集合と同じで、平均値やそのバラツキ等の統計的処理を適用できる数の集まりだと言えます。
さて、個々の株価はこれから上がるのか下がるのか予想はつきませんし、株式会社が倒産してしまうこともあり得ます。倒産してしまえば、投資に継ぎ込んだお金は、戻ってきません。
今、100種類の株を集めた投資信託があったとします。名前は、100銘柄ファンドとでもしておきます。各銘柄を並べて番号をつけ、その代表をiとします。つまり、i=1, 2, 3, …,100 です。
銘柄iの価格は xi とします。ただし、株価は刻々と変化しますので、いつの時点のことなのかをはっきりとさせておかなければなりません。そこで、価格の記号を、xi(t) と書き改めることにします。記号tは、日時の意味です。今日、明日、明後日 ----を順に、t=1, 2, 3 と表すわけです。
株価の変動は、銘柄ごとにバラバラでしょうから、乱数で代用できそうです。ただし、大部分の銘柄は、1日でそれほど大きく変動しないはずです。なかには、極端に上がったり、下がったりするものもあるでしょうが、数は多くはないはずです。そうだとすれば、既出の図で示したような、乱数の平均値が使えます。この値を、乱数の頭文字をとって、rとしておきます。その値は刻々と、つまり使うたびに変わっていくものとします。
株価の変動にはプラスもマイナスもありますので、乱数を利用するために、乱数は-1から1までの間だけを変化するものとします。この乱数をr*と書くことにします。
実際の株価変動がどれくらいになるかは、千差万別ですから、一概にはいえません。そこで1日の最大変動幅を-b円から+b円と決めておきます。これに乱数を掛けて、br*とすればよいことになります。
一方、tは日時ですから、ある日をtとすれば、その次の日はt+1です。しがって、1日でおこる株価の変動分を考えると、
xi(t+1)-xi(t)=br* …①
という関係式が成り立つことになります。これで、株価の推移を表す簡単な数式モデルができたことになります。もちろん、株価変動の雰囲気だけを真似たもので、実際の予測ができるわけではありません。
ここで、①式のような数式の形について、少し掘り下げておきます。株価変動を具体的に書けば、
xi(2)-xi(1)=br*
xi(3)-xi(2)=br*
xi(4)-xi(3)=br*
…
…
と続いていくものです。変化した分を考えるだけで、複雑な出来事を数式で再現することができたのです。
日々の株価は、基本的に一定の割合aで上昇し、それに、予期できない変動br*が加わったもの、と考えることができます。しかも株価は時間とともに、かなり複雑に変化していますから、厳密に考えれば、aも定数ではなさそうです。結局、aもbも時間とともに変化し、かつ株価にも影響されているはずです。
さて、個々の株価の変動については、乱数を使って計算しても、あまり意味がありません。しかし、平均値なら話は違います。
ここで、100銘柄の平均値の推移を求めてみます、平均値をXバーで表わすことにすれば、
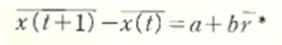
となります。ただし、aとbはとりあえず変化しないもの、としておきます。ここで、乱数で作った図を思い出してください。個々の乱数はバラバラでも、たくさん集めると規則性が出てくる、という話でした。個々の株価は、もちろんデタラメに変動しているわけではありません。ただ、予測がつかないという意味です。
したがって、この話のように、たくさんの銘柄を考える場合には、乱数であっても現実に近い答えが期待できるはずです。つまり、銘柄数が多くなるにつれ、r*=0に近づいて行くはずです。結局は、ほぼ、
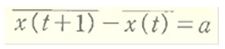
となり、個々の株価変動は消えしまうのです。
ファンドは、最初1万円で売り出されるのが普通です。その後、含まれている株の市場価格に比例して、上がったり、下がったりしていきます。従って、ここまで考えてきた100銘柄の平均値は、そのままファンドの価格と考えてもよいことになります。r*は、株価変動の不確かさを表しています。金融取引ふうにいえば、リスクです。そのリスクが、ファンドの価格から消えてしまうことがわかりました。ここが、個々の株の売買と大きく異なる点です。
もちろん、ファンドがつねに値上がりするわけではありません。この話が成り立つのは、あくまで、数年から数十年と、長期的に考えた場合に限ります。ちなみに、投資信託は、ファンド・マネージャーと呼ばれる専門家の個性で組み立てられ、運用されています。運用と言うのは、ファンドの価格が少しずつ値上がりするように、日々、中身を入れ替えることです。つまり、ファンドの内容にも個性があるということです。外国の優良企業と国債を組合せたもの、日本で急上昇している中小企業の株を集めたものなどです。なかには、あえて上がり下がりの激しい開発途上国の株だけを集めたものなどもあります。さらに、不動産ファンドにしたというユニークなものや、分配型のファンドもあります。
こうなると、ある時期、特定の種類のファンドだけが、集中的に値下がりしたりする危険性も出てきます。従って、たとえば投資信託であっても、1つだけに大金を注ぎ込むのは危険かもしれません。種類の異なる複数のファンドにお金を分散すれば、リスクも一層小さくなるのではないでしょうか。
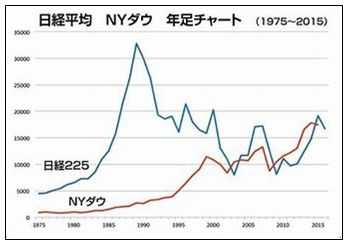
ただし、ファンドの多くは、日経平均やニューヨーク・ダウに連動して価格が変動するように、運用されています。そのほうが、購入者にとっても安心だからです。ということは、いろいろなファンドが一斉に値下がりするということもあるということです。そうであれば、同一範疇内で種類の異なるファンドに分散投資しても意味がありません。そこで考えられるのが、性格の異なる商品、すなわち株式の投資信託、REITの投資信託、金の投資信託に分散投資する方法が考えられます。結局、安全な投資信託とポートフォリオの観点からの分散投資をやりなさいという結論に達します。
今回は、岡田正彦著「考える力がつくやさしい数学」を参考に、投資信託はどうして安全なのかを数学的にひも解いてみました。非常に分り易いと感じましたが皆さんはいかがでしょうか。